Résoudre le jeu snake, deuxième essai: ES6 et ReactJS

Après avoir développé un solveur de jeu snake en Python avec A*, mon stage de découverte de nouveaux langages se poursuit ; je passe maintenant à ES6 et ReactJS avec un algorithme différent. Le résultat est embarqué ci-dessous, cliquez sur "start" pour voir votre navigateur guider le serpent. Dans 80% des cas, il gagne la partie. Vous pouvez également modifier la taille de la grille.

ReactJS, premier contact

Première chose à faire, comprendre le fonctionnement de ReactJS, pour ça je regarde les vidéos de egghead.io qui m'ont beaucoup aidé.

J'entends parler de virtualDOM, de jsx de state et props, après avoir compris quelques notions je reprends un de mes anciens boilerplate AngularJS basé en partie sur celui de marmelab que j'adapte à ReactJS. Il est configuré avec de l'ES6, le bundler webpack et un makefile pour permettre à n'importe qui d'installer et d'utiliser le projet sans nécessairement avoir de connaissances.

De ce que j'ai compris, au lieu de travailler directement avec le DOM, ReactJS utilise un VirtualDOM qui modifie à chaque changement d'état uniquement la partie modifié du DOM, ce qui permet un gros gain en terme de performance.

L'appui des autres développeurs marmelab, qui utilisent ReactJS au quotidien, m'a grandement aidé à mettre le pied à l'étrier.

Voici à quoi ressemble le composant React principal qui contient la boucle de jeu :

const game = new Game(config.size);

class App extends React.Component {
  constructor(props) {
    super(props);

    this.state = {
      grid: game.grid,
      score: game.score,
      snake: game.snake,
    };
  }

  componentWillMount() {
    this.tick();
  }

  tick() {
    setTimeout(() => {
      try {
        const nextMove = getNextMove(game);
        game.nextTick(nextMove);
        this.setState({
          grid: game.grid,
          score: game.score,
          snake: game.snake,
        });
        this.tick();
      } catch (e) {
        console.log(e.message);
        console.log("Finish !");
      }
    }, config.speed);
  }

  render() {
    return (
      <div>
        <div className="score">Score: {this.state.score}</div>
        <Grid grid={this.state.grid} snake={this.state.snake} />
      </div>
    );
  }
}

ReactDom.render(<App />, document.getElementById("app"));

L'algorithme de résolution

Alors il existe bien une solution pour finir le jeu à tous les coups, une personne s'est d'ailleurs amusée à détourner une démo jQuery du jeu snake avec ce script. Il se sert du cycle hamiltonien et répète toujours le même chemin en passant par toutes les cases. Mais c'est très ennuyeux et pas du tout naturel.

Le but ici est de résoudre le jeu avec un algorithme qui se rapproche un peu plus d'un gameplay humain.

Je me suis basé sur les spécifications données par François pour développer un algorithme de parcours en largeur (ou Breadth First Search en anglais). On peut aussi voir cette approche comme une exploration "brute force" de tous les mouvements possibles, en tenant compte du temps. On peut schématiser l'algorithme sous forme d'un arbre où chaque branche représente un chemin et détient un score{: style="color: red"} :

A chaque fois que le serpent doit avancer, on explore les 3 possibilités de mouvement (parce qu'il ne peut pas revenir en arrière) parmi (G)auche, (D)roite, (H)aut, et (B)as. On calcule alors la position du serpent au coup d'après, en faisant avancer sa queue aussi. On calcule un score pour chaque position. Et on recommence : on réexamine les 3 positions possibles pour chaque position. Et ainsi de suite, en augmentant le nombre de "ticks" (c'est-à-dire le nombre de coups d'avance).

La fonction de calcul du score d'une position s'appelle getMoveScore :

export function getMoveScore(sizeGrid, move, snake, apple, tick) {
  const newSnake = moveSnake(snake, apple, move);

  if (isSnakeHeadAtPosition(newSnake, apple)) {
    if (!isSnakeHasFreeSpace(snake, sizeGrid)) {
      return 0;
    }

    return (1 / tick) * 100;
  }

  if (isCollide(newSnake, sizeGrid)) {
    return 0;
  }

  return 1;
}

• Si le serpent tombe sur la pomme le score est de 100 multiplié par (1 / tick) pour privilégier le chemin le plus court.
• Si le serpent tombe sur la pomme mais qu'il n'y pas de mouvement possible autour d'elle le score est de 0.
• Si le serpent rencontre un obstacle le score est de 0.
• Si le serpent ne rencontre aucun des cas précédents le score est de 1.

Une fois l'ensemble des chemins possibles listé, le serpent se dirige vers le chemin ayant le meilleur score. Le serpent évite ainsi les obstacles et privilégie les chemins les plus courts et ceux où se situe la pomme.

Efficacité de l'algorithme

Si l'on compare cet algorithme avec un comportement humain, on remarque que contrairement à l'humain le serpent n'est pas effrayé à l'idée de suivre sa queue de très près. De plus, il est capable d'éviter de courir droit vers la pomme s'il sait que ça va le faire perdre - prenant dans ce cas un large détour.

En ce sens, on a l'impression d'assister au travail d'une Intelligence Artificielle - même si on est loin des travaux de Google en la matière (DeepMind sait gagner à 49 jeux Atari sans apprentissage guidé).

Le serpent peut cependant mettre plus de temps sur des mouvement évidents, comme en début de partie où la pomme se trouve juste en face de lui. C'est une différence marquante avec l'algorithme de pathfinding A star, qui va immédiatement aller sur la pomme. Et sur les grandes grilles, si nombre de cases qui le sépare de la pomme est supérieur au nombre de ticks, alors aucun chemin ne sera privilégié, et il prendra une direction aléatoire - d'où un comportement erratique.

Test-Driven Development

Comme c'est la règle chez marmelab, j'ai développé en TDD tout le long du projet. Les avantages sont nombreux :

• On écrit un code plus fiable.
• On évite les régressions.
• On peut développer et tester chaque nouvelle feature indépendamment du reste.
• On comprend mieux les spécifications du programme et n'importe qui peut comprendre le code simplement en regardant les tests.
• Le code est mieux architecturé, moins couplé

Voici un exemple de test unitaire sur le comportement du serpent après avoir mangé une pomme.

describe("apple", () => {
  /*
        [ 1, 1, 1, 2, 0 ]
        [ 0, 0, 0, 0, 0 ]
        [ 0, 0, 0, 0, 0 ]
        [ 0, 0, 0, 0, 0 ]
        [ 0, 0, 0, 0, 0 ]
    */
  it("should expand snake after eating the apple", () => {
    const game = new Game([5, 5]);
    const snakeSize = game.snake.length;

    game.nextTick(RIGHT);
    const newSnakeSize = game.snake.length;

    assert.notEqual(snakeSize, newSnakeSize);
  });
});

Comme vous pouvez le voir, j'ai ajouté en commentaire un visuel de la grille avec les placements du serpent et de la pomme :

• 0 pour les cases vides
• 1 pour le serpent
• 2 pour la pomme

L'algorithme étant à première vue compliqué, j'ai pu me rendre compte que le TDD m'a grandement simplifié la tâche. A chaque fois que le serpent s'est retrouvé dans une impasse, j'ai ajouté puis validé un test unitaire. Ainsi, je peux avoir une vue sur chaque cas particulier et avancer sans faire de retour en arrière.

Programmation fonctionnelle

Après avoir fait quelques heures de JavaScript en programmation orientée objet, François m'a initié à la programmation fonctionnelle. Une expérience unique qui m'a permis d'avoir une architecture lisible avec des fonction immutables.

En effet, ce paradigme évite les effets de bords. Pour mieux comprendre, voici une comparaison entre une simple boucle for et un Array.prototype.forEach().

var array = [1, 2, 3];

for (var i = 0, length = array.length; i < length; i++) {
  // ...
}

Dans l'exemple ci-dessus, les variables i et length sont disponibles dans le scope global, et peuvent potentiellement être modifiées.

[1, 2, 3].forEach(function(item, index, array) {
  //
});

Alors qu'avec l'utilisation d'un forEach, on ne crée pas de variable pour faire une boucle, on évite ainsi les effets de bords.

Aussi, j'ai pris l'habitude de tout déplacer dans des fonctions courtes et correctement nommées afin de remplacer les commentaires par des appels de fonctions.

// Avant

// Check if this is the last move of the snake
if (snake.length === game.surface - 1) {
  // ...
}

// Après

export function isLastMove(snake, game) {
  return snake.length === game.surface - 1;
}

if (isLastMove(snake, game)) {
  // ...
}

Le code est bien plus lisible, bien plus testable, et plus facile à débugguer.

Optimisation 1: Utilisation des arrays typés

Pour stocker les résultats de l'exploration de l'algorithme, on utilisait dans un premier temps un tableau d'objets qui contenait l'ensemble des chemins possibles (moves) associés à un score. Les chemins étaient des listes de positions choisies pour la tête [x, y] :

const possibleMoves = getPossibleMoves(snake, sizeGrid);
// [ [ 0, 3 ], [ 1, 2 ] ]

const movesScores = [];
possibleMoves.forEach(move => {
  const moveScore = getMoveScore(sizeGrid, move, snake, apple);
  movesScores.push({ moves: [move], score: moveScore });
});

/* Output:
[
    { moves: [ [ 0, 3 ], [0, 4], [1, 4], [2, 4] ], score: 0 },
    { moves: [ [ 0, 3 ], [1 .3], [2, 3], [3, 3] ], score: 1 },
    { moves: [ [ 0, 3 ], [1 .3], [1, 4], [2, 4] ], score: 1 }
]
*/

Au-delà de 5 ticks, le programme bloquait à cause d'une consommation mémoire trop importante.

Pour optimiser cela, on a changé de structure de données, pour utiliser des tableaux typés, plus précisément des Uint8Array.

La taille des Uint8Array est fixée à seulement 8 bits, contrairement aux autres Array qui ont par défaut 64 bits, ce qui fait la différence en terme de performance. Il faut juste faire attention à ne pas les confondre avec les Array classiques, car certaines méthodes comme push() et pop() ne sont pas disponible pour les Array typés.

Problème: un chemin est un tableau de moves, qui sont eux-mêmes des tableaux. Uint8Array ne permet de stocker que des données scalaires.

L'amélioration consiste à séparer les 'moves' des 'score' dans des Uint8Array séparés, et de ne plus avoir de 'moves' sous forme de position [x, y], mais de direction.

const [UP, RIGHT, DOWN, LEFT] = [0, 1, 2, 3];

const possibleMoves = getPossibleMoves(snake, sizeGrid);
// [1, 2]

let scores = new Uint8Array(possibleMoves.length);
// Uint8Array { '0': 0, '1': 1 }

let moves = possibleMoves.map((move, index) => {
  scores[index] = getMoveScore(sizeGrid, move, snake, apple);
  return new Uint8Array([move]);
});
// [ Uint8Array { '0': 1 }, Uint8Array { '0': 2 } ]

On possède désormais un Uint8Array pour les scores, et un tableau de Uint8Array pour les moves.

Cette optimisation réduit très significativement la consommation mémoire, et nous fait gagner 3 ticks supplémentaires dans l'exploration des chemins, pour un maximum de 8 ticks.

Optimisation 2 : détection et optimisation des fonctions les plus utilisées

Pour maximiser les performances de l'algorithme, j'ai aussi utilisé les fonctionnalités de DevTools (disponible nativement sur chromium).

Les outils "Timeline" et "Profiles" enregistrent et analysent l'activité de mon application pour ensuite investiguer les problèmes de performance (CPU et mémoire) :

• "Timeline"

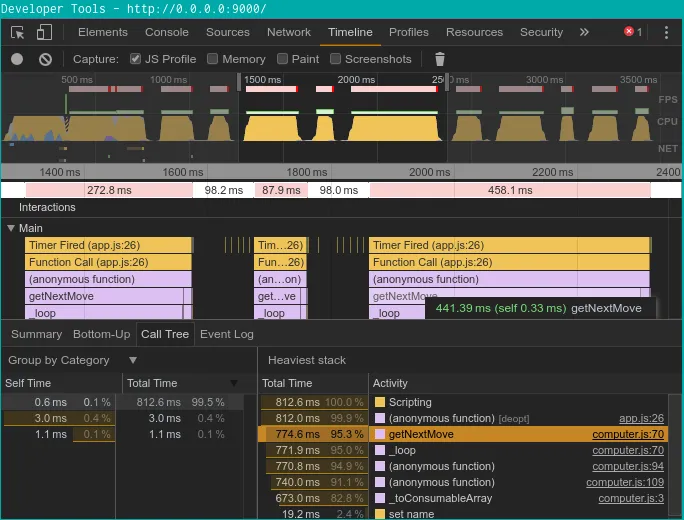
• "Profiles"

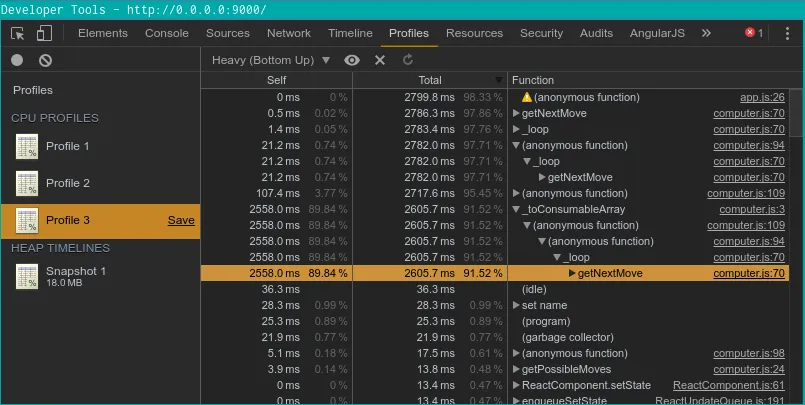
A partir de là, il devient facile de se concentrer sur les fonctions les plus consommatrices et de les optimiser à l'extrême, parfois au prix d'un retour à la programmation impérative (car le fonctionnel en JavaScript n'est pas aussi optimisé).

Optimisation 3: Ajuster la profondeur sur le temps d'exécution

On a fixé la taille de l'exploration, d'abord à 5 ticks, puis à 8 ticks :

const MAX_TICK = 8;

Lorsque le jeu commence, le nombre de possibilités est très élevé: à chaque tick, on a effectivement 3 positions à explorer. On se retrouve avec des tableaux de plusieurs milliers d'entrées (3^tick), coûteux en mémoire et en CPU. En fin de partie, quand le serpent entre dans des "couloirs" formés par son propre corps, les ticks sont moins coûteux, puisqu'il n'y a qu'une ou deux positions possibles. Sur une grille de 5x5, le délai de résolution reste correct. Mais dès lors que l'on essaie une grille plus grande, le serpent peine à démarrer et il faut parfois attendre entre 2 et 5 secondes pour chaque déplacement.

Une optimisation supplémentaire consiste à ajuster le nombre de ticks en fonction du temps passé par l'algorithme pour la résolution de la dernière position. Par exemple, si l'algorithme était à 8 ticks maximum et a mis plus de 5 secondes pour calculer toutes les positions, on diminue à 7 ticks pour le coup d'après. A l'inverse, s'il était à 5 ticks et qu'il a mis moins d'1 seconde pour calculer toutes les positions, on augmente le nombre de ticks à 6.

Ainsi, non seulement on rend les mouvements du serpent plus rapides (surtout en début de partie), mais on augmente significativement le nombre de ticks en fin de partie, là où il est important de voir le plus à l'avance possible.

Dessiner le serpent: merci CSS !

Pour dessiner le serpent j'ai créé 3 images sur photoshop :

• La tête
• Le corps pour les mouvements droits
• Le corps pour les mouvements de côtés

On les oriente de 90° ou 180° en CSS selon la position du serpent, et le tour est joué.

Pour positionner correctement chaque image, je parcours tous les éléments du serpent et vérifie chaque élément voisin pour en déduire l'image à utiliser :

export function getBlock(snake, index) {
  const prevPosition = getDirection(snake[index], snake[index - 1]);
  const nextPosition = getDirection(snake[index], snake[index + 1]);

  if (
    (prevPosition === LEFT && nextPosition === RIGHT) ||
    (prevPosition === RIGHT && nextPosition === LEFT)
  ) {
    return "horizontal";
  }

  if (
    (prevPosition === UP && nextPosition === DOWN) ||
    (prevPosition === DOWN && nextPosition === UP)
  ) {
    return "vertical";
  }

  if (
    (prevPosition === UP && nextPosition === RIGHT) ||
    (prevPosition === RIGHT && nextPosition === UP)
  ) {
    return "up_right";
  }

  if (
    (prevPosition === DOWN && nextPosition === LEFT) ||
    (prevPosition === LEFT && nextPosition === DOWN)
  ) {
    return "down_left";
  }

  // ...
}

export function getBlocks(snake) {
  return snake.map((block, index) => getBlock(snake, index));
}

Conclusion

Pour conclure, si on compare l'algorithme A star anciennement utilisé avec celui-ci, on peut dire que A star recherche le chemin vers la pomme plus rapidement, mais il calcule seulement le plus court chemin sans faire de tri parmi les solutions possibles.

Le nouvel algorithme quant à lui explore tous les chemins possibles et sélectionne le meilleur. On se retrouve donc avec un algorithme moins performant certes mais plus fiable. Il évite les obstacles et se projette plus loin que la pomme. Il résout plus de grilles que le A star.

Il existe cependant un cas particulier non résolu, où le serpent peut se retrouver enfermé si après avoir tourné dans une zone potentiellement dangereuse une nouvelle pomme apparait dans cette même zone après avoir mangé la première. Là, c'est la règle du jeu qu'il faut changer : la pomme ne devrait apparaitre que dans des zones où le serpent peut aller la chercher sans se suicider.

Une solution pour améliorer l'AI serait de paralléliser le traitement de la recherche de chemin pour gagner en performance et obtenir un nombre de ticks plus élevé. C'est possible dans un navigateur avec les ServiceWorkers.

Il est également possible d'améliorer la fonction de score, par exemple pour pondérer chaque position en fonction du nombre de mouvements possibles, ce qui permet de disqualifier les positions qui "enferment" le serpent.

Du point de vue développement j'ai trouvé que l'utilisation de l'ES6 facilite l'usage de JavaScript. Il est aussi agréable pour moi de développer dans ce langage qu'en Python. J'ai de ce fait beaucoup évolué en ES6, ainsi qu'en programmation fonctionnelle.

Ce projet a été très enrichissant pour moi, je découvre de plus en plus les avantages du TDD. Il existe sûrement encore des améliorations côté ReactJS, peut être en intégrant Redux que je n'ai pas eu le temps d'explorer.

Les code review de Marmelab sont toujours très instructives. Chaque morceau de code est vérifié et commenté, me permettant ainsi d'alléger mon code au maximum, et d'obtenir une meilleure lisibilité.

Si le code source vous intéresse, il est open-source. Rendez-vous sur le repo GitHub marmelab/snake_solver_two.